
Pineau, J.C., 2020. Prédiction de la masse grasse totale et du pourcentage de graisse chez les hommes adultes: étude comparative avec les modèles prédictifs élaborés en épidémiologie. Antropo, 43, 1-10. www.didac.ehu.es/antropo
Prédiction de la masse grasse totale et du pourcentage de graisse chez les hommes adultes: étude comparative avec les modèles prédictifs élaborés en épidémiologie
Prediction of total body fat and percentage fat in adult men: comparative study with predictive models developed in epidemiology
Jean-Claude Pineau
CNRS, Université de Paris, BABEL, 75012, Paris France. jc.pineau@numericable.fr
Mots-clés: Composition corporelle, DXA, Anthropométrie, Epidémiologie
Key-words: Body composition, DXA, Anthropometry, Epidemiology
Résumé
La présente étude a pour principal objectif d'utiliser et de valider sur notre échantillon les équations prédictives de la masse grasse et du pourcentage de graisse élaborées dans les études épidémiologiques. Les équations prédictives de la masse grasse sont obtenues à partir de l'âge et des mesures anthropométriques: poids, stature, tour de taille et BMI.
L'échantillonnage est composé de 120 hommes adultes âgés de 18 à 82 ans pour lequel la masse grasse totale est obtenue par absorptiométrie DXA.
Des différences significatives de la masse grasse moyenne et du pourcentage de graisse moyen sont observés entre notre modèle prédictif et ceux élaborés au plan épidémiologique. Toutefois, les variances estimées de la masse grasse n'étant pas significatives, nous avons introduit un terme correctif compte tenu des différences de logiciel et de vitesse de balayage entre les appareils DXA. Il existe alors de fortes corrélations (r>0,98) entre les valeurs prédictives observées entre les modèles issus des études épidémiologiques et notre modèle. De plus, les écarts individuels de masse grasse sont comparables.
Cependant, un modèle prédictif élaboré sur un plus faible effectif n'est pas applicable à notre échantillon car il induit une surestimation significative des valeurs moyennes et des écarts-types ce qui augmente significativement les écarts individuels de masse grasse.
En conclusion cette étude montre que l'utilisation des équations prédictives de la masse grasse et du pourcentage de graisse élaborées à partir de mesures anthropométriques au plan épidémiologique sont tout à fait applicables à différents échantillons pour lesquels les mêmes mesures anthropométriques ont été relevées.
Abstract
The main objective of this study is to use and validate on our sample, the predictive equations of fat mass and fat percentage developed in epidemiological studies. Predictive equations of fat mass are obtained from age and anthropometric measurements: weight, height, waist circumference and BMI. The sample consists of 120 adult males aged 18-82 years in which total fat mass is obtained by DXA.
Significant differences in mean fat mass and average fat percentage are observed between our predictive model and those developed epidemiologically. However, since the estimated fat mass variances are not significant, we introduced a corrective term taking into account the differences in software and scan speed between DXA devices. There are then strong correlations (r>0,98) between the observed predictive values between the models from the epidemiological studies and our model. In addition, the individual fat mass differences are equivalent.
However, a predictive model developed on a smaller size is not applicable to our sample as it induces a significant overestimation of mean values and standard deviations which significantly increases individual fat mass differences.
In conclusion, this study shows that the use of predictive equations of fat mass and fat percentage based on epidemiological anthropometric measurements is quite applicable to different samples for which the same anthropometric measurements have been identified.
Introduction
L'excédent de masse grasse est un facteur de risque pour de nombreuses maladies chroniques pouvant induire une mortalité prématurée (Must et al., 1999; Willett et al., 1999; Olshansky et al., 2005). L’obésité mondiale a presque doublé au cours des trois dernières décennies (WHO, 2013). En France, la prévalence de l'obésité chez les adultes est de 11,3% soit environ 3,5 millions de personnes. L'obésité est souvent associée avec le risque cardiovasculaire et sanitaire grave (Wormser et al., 2011).
L'absportiométrie (DXA) est une méthode de référence reconnue pour mesurer la composition corporelle dans les études transversales et longitudinales (Kelly et al., 2005; Newman et al., 2005). Toutefois, cette technique présente l'inconvénient d'une exposition aux rayonnements avec un coût relativement élevé et une accessibilité limitée. Pour cette raison, de nombreuses études ont proposé d'établir des équations prédictives de la masse grasse (MG kg) et du pourcentage de graisse (MG%) à partir de différentes variables: âge, sexe, mesures anthropométriques versus l'absorptiométrie DXA (Mills et al., 2008; Gallagher et al., 2000; Van der Ploeg et al., 2003).
Des études épidémiologiques récentes ont établi des équations prédictives de la masse grasse (MG) et du pourcentage de graisse (MG%) à partir de différentes variables; âge, sexe, dimensions anthropométriques en utilisant l'absorptiométrie DXA comme mesure de référence (Lee et al., 2017; Héo et al., 2013). L'intérêt de ces études porte sur un nombre élevé de sujets couvrant ainsi une grande variabilité des mesures de masse grasse (MG) et des dimensions anthropométriques.
La présente étude a pour principal objectif d'utiliser les équations prédictives de la masse grasse et du pourcentage de graisse élaborées dans ces études épidémiologiques en vue d'effectuer des estimations de MG et de MG% sur notre échantillon de sujets afin de connaître la précision des valeurs moyennes et individuelles de MG et de MG%.
En fonction des résultats obtenus, des facteurs correctifs seront effectués afin d'améliorer les prédictions obtenues.
Matériels et méthodes
Cette étude a été réalisée dans un service de nutrition d'un centre hospitalier universitaire. Tous les patients ont signé un formulaire de consentement écrit conformément à la Déclaration d’Helsinki révisée en 2013. La majorité des patients sont Caucasiens. Les critères d’inclusion concernent uniquement les patients qui ont donné leur consentement écrit après avoir reçu une lettre d’information sur le recueil des mesures. Les patients inscrits étaient en bonne santé et présentaient une grande variabilité de BMI = Poids (kg)/stature²(m) et de masse grasse corporelle totale. Les critères d’exclusion s’appliquent aux patients souffrant de troubles d’hydratation, d’insuffisance cardiaque, d’insuffisance rénale, de grossesse, de diurétiques, de corticoïdes ou d’antidépresseurs. Les patients atteints de cancer qui prennent des médicaments et qui refusent de signer un consentement éclairé sont également exclus.
L'échantillonnage est composé de 120 hommes adultes âgés de 18 à 82 ans. Pour chaque sujet examiné, nous avons relevé la masse grasse totale (MG DXA) et le pourcentage de graisse (MG% DXA) mesuré par absorptiométrie DXA avec un Hologic QDR-4500 W (version 11.25, Hologic Bedford, Mass USA). La technique DXA, qui scanne le corps entier avec un faisceau de rayons X à deux niveaux d’énergie (70 et 100 Kev) est une méthode de référence pour mesurer la masse grasse, la masse maigre et la teneur en minéraux. Le sujet est en position couchée pendant 7 minutes et l’exposition au rayonnement est très faible. Le poids du sujet est calculé avec une précision inférieure à 1 %. Le résultat de la composition corporelle est disponible immédiatement après chaque examen.
Les mesures anthropométriques recueillies sont celles qui sont utilisées dans les équations prédictives établies par Lee et al. (2017) et par Héo et al. (2013). Elles concernent le poids (kg), la stature (cm), le BMI et le tour de taille (cm). Le poids est relevé à 100g près à l'aide d'une balance Tanita, la stature est mesurée à 5 mm près avec une toise anthropométrique et le tour de taille a été relevé avec un ruban métrique au niveau du bord latéral supérieur de la crête de la hanche à 0,1 cm près.
Modèles prédictifs utilisés
Différents modèles de régression linéaire multiple donnant une estimation de la masse grasse totale (MG) et du pourcentage de graisse (MG%) versus DXA ont été établis en fonction des variables suivantes: âge, poids, stature, tour de taille pour Lee et al. (2017) et du BMI pour Héo et al. (2013). Ces équations ont été utilisées pour effectuer une estimation de MG (kg) et de MG% sur notre échantillon composé de 120 sujets. De plus, nous avons élaboré un modèle prédictif de MG et de MG% à partir de ces différentes variables versus l'absportiométrie DXA. Les résultats sont regroupés dans le tableau 1 dans lequel nous avons précisé les valeurs de R² et de l'erreur standard d'estimation (SEE).
|
Variable dépendante |
Age (an) |
Poids (kg) |
Stature (cm) |
Tour de taille (cm) |
BMI (kg/m²) |
Cte |
R² |
SEE |
|
MG(kg) |
|
|
|
|
|
|
|
|
|
1-Pineau n =120 |
0,0016 |
0,256 |
-0,251 |
0,312 |
|
11,49 |
0,95 |
2,35 |
|
2-Lee et al. n = 5329 |
-0,009 |
0,226 |
-0,08 |
0,387 |
|
-18,59 |
0,9 |
2,6 |
|
MG% |
|
|
|
|
|
|
|
|
|
3-Pineau n=120 |
0,004 |
-0,048 |
-0,191 |
0,454 |
|
15,18 |
0,88 |
2,61 |
|
4-Lee et al. n=5329 |
0 |
-0,08 |
-0,07 |
0,48 |
|
0,02 |
0,73 |
3,07 |
|
MG(kg) |
|
|
|
|
|
|
|
|
|
5-Pineau n =120 |
|
|
|
|
1,63 |
-24,86 |
0,92 |
2,86 |
|
6-Héo et al. n =3347 |
|
|
|
|
1,77 |
-24 |
0,86 |
3,89 |
Tableau 1. Modèles prédictifs d'estimation de MG (kg) et MG% selon les résultats des enquêtes épidémiologiques de Lee et al. (2017) et Héo et al. (2013) en fonction des variables anthropométriques.
Table 1. Predictive estimation models of MG (kg) and MG% from anthropometric variables based on epidemiological studies of Lee et al. (2017) et Héo et al. (2013).
Analyse statistique
L'analyse statistique porte sur la comparaison des valeurs moyennes et écart type des variables anthropométriques à partir du test "t" de Student et du test de Fisher pour comparer les variances. Les coefficients de détermination R² sont précisés ainsi que l'erreur standard d'estimation selon l'expression : SEE = s Ö1- R² où s représente l'écart type de MG ou de MG%. Pour chaque test, p<0,05 est considéré comme le seuil de signification.
Résultats
Les valeurs moyennes et écarts-type des mesures anthropométriques des échantillons retenus sont regroupées dans le tableau 2.
On observe pas de différence significative entre les mesures anthropométriques de notre échantillon versus la population de Lee et al. (2017). A l'inverse on observe des différences significatives des mesures anthropométriques, de MG DXA et MG% DXA entre notre échantillon et la population de Héo et al. (2013).
On constate des différences significatives des valeurs de MG DXA et de MG% DXA entre les trois cohortes retenues.
|
|
1-Pineau n =120 |
2-Lee et al. n = 5239 |
3-Héo et al. n = 3347 |
"t" 1 vs 2 |
"t" 1 vs3 |
|
|
|
m ± s |
m ± s |
m ± s |
p |
p |
|
|
Age (an) |
41,6 ± 17,7 |
42,7± 22,4 |
45,4 ± 16,5 |
0,59 |
0,01 |
|
|
Poids (kg) |
82,0 ± 18,8 |
82,9 ± 22,4 |
88,3 ± 18,7 |
0,66 |
<0,01 |
|
|
Stature (cm) |
175,2 ± 7,4 |
176,5 ± 10,9 |
177,5 ± 7,2 |
0,19 |
<0,01 |
|
|
BMI (kg/m²) |
26,7 ± 5,8 |
26,6 ± 5,8 |
28,0 ± 5,5 |
0,85 |
0,01 |
|
|
Tour de taille (cm) |
95,9 ± 16,8 |
95,8 ± 19,5 |
100,4± 19,5 |
0,95 |
0,01 |
|
|
MG DXA (kg) |
18,6 ± 9,9 |
22,7 ± 11,8 |
26,0 ± 10,4 |
<0,01 |
<0,01 |
|
|
MG% DXA |
21,4 ± 7,5 |
26,5 ± 8,0 |
- |
<0,01 |
- |
|
Tableau 2. Valeurs moyennes et écart types des variables anthropométriques, de MG DXA (kg) et de MG% DXA de notre échantillon et des études épidémiologiques.
Table 2. Mean values and standard deviations of anthropometric variables, MG DXA (kg) and MG% DXA of our sample and epidemiological studies.
Modèles prédictifs de MG et de MG% élaborés sur notre échantillon à partir d'enquêtes épidémiologiques
Les équation prédictives de MG et MG% élaborées par Lee et al. (2017) et par Héo et al. (2013) ont été réalisées dans le cadre d'enquêtes épidémiologiques portant sur de grands effectifs. Les valeurs moyennes des estimations de MG et de MG% ainsi que les écart moyens entre les valeurs estimées de MG et MG% avec les valeurs MG DXA et MG% DXA sont regroupées dans le tableau 3.
Nous constatons que les estimations de MG (kg) réalisée sur notre échantillon de 120 sujets à partir des équations de Lee et al. (2017) et de Héo et al. (2013)présentent une surestimation significative des valeurs moyennes mais pas de différences significative des variances.
|
Equations utilisées (n=120) |
m ± s |
Ecart |
"t" Student P |
|
MG (kg) |
18,6 ± 9,9 |
|
|
|
MG (kg) estimée Equation 1 |
18,5 ± 9,7 |
-0,07 ± 2,3 |
NS |
|
MG (kg) estimée Equation 2 |
22,7 ± 10,4 |
4,1 ± 2,7 |
<0,01 |
|
MG (kg) estimée Equation 5 |
18,6 ± 9,5 |
0,04 ± 2,8 |
NS |
|
MG (kg) estimée Equation 6 |
23,2 ± 10,4 |
4,6 ± 2,9 |
<0,01 |
|
MG % |
21,4 ± 7,5 |
|
|
|
MG% estimée Equation 3 |
21,5 ± 7,0 |
0,1 ± 2,6 |
NS |
|
MG% estimée Equation 4 |
27,2 ± 6,8 |
5,8 ± 2,7 |
<0,01 |
Tableau 3. Estimations de MG (kg) et MG% effectuées sur notre échantillon (équations 1, 5 et 3) et celles obtenues à partir de les équations 2 et 4 de Lee et al. (2017) et l'équation 6 de Héo et al. (2013).
Table 3. Estimates of MG (kg) and MG% from our sample (equations 1, 5 and 3) and those obtained from equations 2 and 4 of Lee et al. (2017) and equation 6 of Héo et al. (2013).
Introduction d'un terme correctif pour rétablir le biais entre les estimations moyennes observées
Les équations 2 et 4 de Lee et al. (2017) font apparaitre une surestimation significative respectivement de la masse grasse MG et du pourcentage de graisse MG%.
Afin de corriger cette surestimation, nous avons relevé la masse grasse et le pourcentage de graisse de 5 sujets dont le BMI (26,3 ≤ BMI≤ 27,0) est en moyenne proche du BMI moyen de Lee égal à 26,6 kg/m². Dans ces conditions, nous obtenons une masse grasse estimée par l'équation 2 de Lee de 22,2 kg ce qui correspond à une surestimation de 4,2 kg vis à vis de la masse grasse DXA de notre étude qui est de 18,0 kg.
Il faut donc introduire un facteur correctif de -4,2 kg dans la formule 2 de Lee et al. (2017) pour réajuster la moyenne de MG (kg) estimée.
Nous avons représenté graphiquement la droite de régression entre les valeurs obtenues par l'équation 1 avec celles de l'équation 2 corrigée (Figure 1). La corrélation est très élevée (r²=0.986). De plus nous avons représenté graphiquement les écarts individuels obtenus à partir des équations 1 et 2 corrigée en fonction de la masse grasse DXA des 120 sujets (Figure2). Nous constatons une relative superposition des écarts avec une amplitude comprise dans 95% des cas entre ± 6 kg.
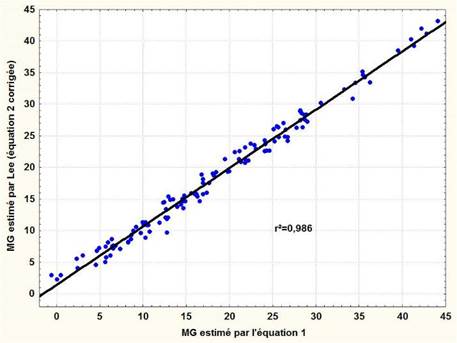
Figure 1. Relation entre la MG (kg) estimée par l'équation 2 corrigée de Lee et al. (2017) et l'équation 1 de notre échantillon de 120 sujets.
Figure 1. Relationship between the MG (kg) estimated by equation 2 corrected of Lee et al (2017) and equation 1 of our sample of 120 subjects.
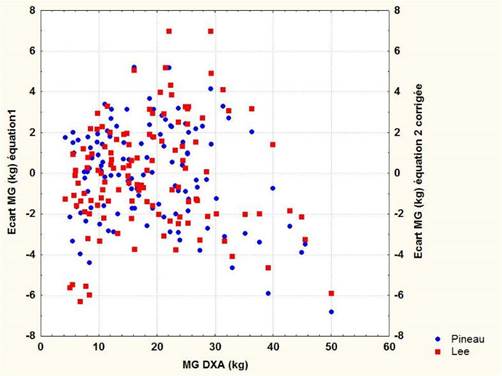
Figure 2. Ecarts individuels entre les estimations de la MG (kg) obtenues par l'équation 1 et l'équation 2 corrigée de Lee et al. (2017) en fonction de la MG DXA (kg) de notre échantillon.
Figure 2. Individual deviations between the MG estimates (kg) obtained from equation 1 and equation 2 corrected of Lee et al. (2017), based on the MG DXA (kg) of our sample.
De la même façon avec les 5 sujets précédents, on obtient une estimation de MG% DXA de Lee et al. (2017) égale à 28 % et une valeur de 22,15% avec notre estimation, soit une surestimation de la formule de Lee et al. (2017) de 5,85% .
Si l'on introduit un facteur correctif de -5,85 dans l'équation 4 de Lee et al. (2017), on réajuste alors la moyenne de MG% estimée. La figure 3 représente le nuage de corrélation entre les valeurs obtenues par l'équation 3 et celles de l'équation 4 corrigée. Le coefficient de corrélation est élevé (r =0,989) et nous observons à nouveau une relative superposition des valeurs avec des écarts individuels compris entre ±5 % dans 95% des cas (Figure 4).
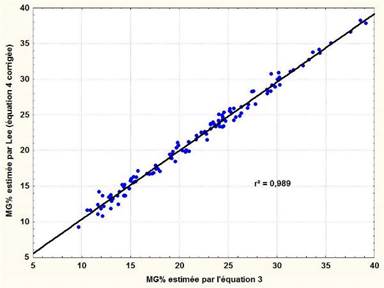
Figure 3. Relation entre MG% de l'équation 4 corrigée de Lee et notre estimation à partir de l'équation 3.
Figure 3. Relation between MG% of Lee’s corrected (equation 4) and our estimate from equation 3.
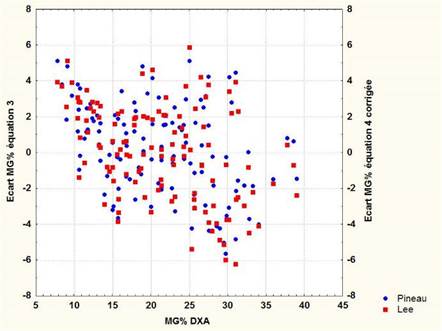
Figure 4. Ecarts individuels entre les estimations de la MG% obtenues par l'équation 3 et l'équation 4 corrigée de Lee et al. (2017) en fonction de la MG% DXA de notre échantillon.
Figure 4. Individual deviations between MG% estimates obtained from equation 3 and equation 4 corrected of Lee et al. (2017), based on the MG% DXA of our sample.
L'équation 6 de Héo et al. (2013) qui fait intervenir uniquement le BMI donne une prédiction de MG (kg) égale à 23,2 kg au lieu de 18,6 kg, soit une surestimation de 4,6 kg. En choisissant 4 sujets dont le BMI est compris entre 27,8 et 28,4 kg/m², on obtient une surestimation de la formule 6 de Héo et al. (2013) de 4,65 kg.
L'équation 6 corrigée de Héo en retranchant 4,65 kg donne à nouveau des écarts individuels proche des écarts obtenus avec la formule 5 sur les 120 sujets (Figure 5).
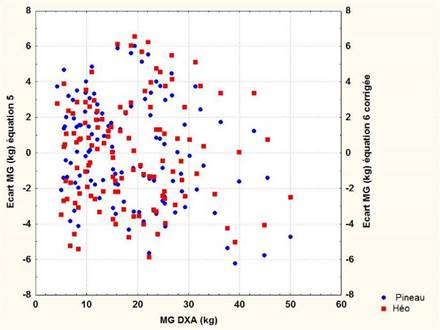
Figure 5. Ecarts individuels entre les estimations de la MG(kg) obtenues par l'équation 5 et l'équation 6 corrigée de Héo et al. (2013), en fonction de la MG DXA (kg) de notre échantillon.
Figure 5. Individual deviations between MG(kg) estimates obtained from equation 5 and equation 6 corrected of Heo et al. (2013), based on the MG DXA (kg) of our sample.
Modèle prédictif de MG et de MG% élaboré sur notre échantillon à partir d'une étude réalisée sur un plus faible effectif
Dans l'étude de Larsson et al. (2006), les auteurs ont établi une régression linéaire entre MG DXA et le rapport Poids(kg)/Stature(en m) sur un échantillon de 274 hommes âgés de 31 à 62 ans. L'équation obtenue est:
MG (kg) = 1,12 Poids/Stature -30,84 (équation 7) (r² = 0,83 et SEE = 3,4 kg).
MG DXA (kg) = 26,0 kg ± 10,4 (n=274).
L'équation 7 appliquée à notre échantillon de 120 sujets donne une valeur de MG estimée = 21,5 kg ± 11,5.
L'écart moyen entre MG estimée et MG DXA est de 2,9 kg ± 3,9. Il existe une différence significative de l'écart moyen (p<0,05) ainsi que des variances (p<0,05) entre l'estimation de Larsson et al. (2006), et celle que nous avons obtenue par l'équation 1.
Si l'on introduit un facteur correctif de 2,9 kg dans l'équation 7, on obtient alors un écart moyen de 0,02 kg ± 3,9.
Les écarts individuels de la formule 7 corrigée de Larsson et al. (2006) présentent une dispersion beaucoup plus grande que celle obtenue par notre équation 1 (Figure 6). La comparaison des variances est significative (p<0,05). En conséquence, le modèle linéaire proposé par Larsson et al. (2006) ne peut s'appliquer à notre échantillon.
Discussion
Dans cette étude nous avons utilisé les équations prédictives de la masse grasse et du pourcentage de graisse en fonction de critères anthropométriques simples qui ont été élaborés au plan épidémiologique à partir de la population américaine. Différentes équations ont été proposés par Lee et al. (2017) et Héo et al. (2013) sur de très grands effectifs respectivement de 5 239 et 3 347 hommes adultes.
Les caractéristiques anthropométriques de notre échantillon de 120 hommes sont tout à fait comparables à celles de Lee. Cependant on observe des différences significatives des valeurs moyennes de MG (kg) DXA et MG% DXA entre ces deux études malgré le fait que les mesures d'absorptiométrie DXA soient relevées par un appareil Hologic QDR 4500 similaire.
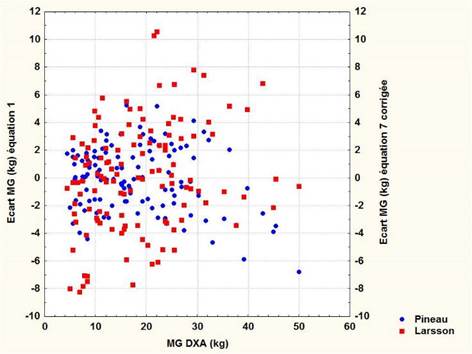
Figure 6. Ecarts individuels entre les estimations de la MG(kg) obtenues par l'équation 1 et l'équation 7 corrigée de Larsson et al. (2006) en fonction de la MG DXA (kg) de notre échantillon.
Figure 6. Individual deviations between MG(kg) estimates obtained from equation 1 and equation 7 corrected of
Larsson et al. (2006), based on the MG DXA (kg) of our sample.
La plupart des études comparant les mesures de la composition corporelle entre différents appareils DXA ont établi qu’une nouvelle équation obtenue par validation croisée est nécessaire parce que l’appareil diffère sur le plan de l’étalonnage, du logiciel et de la vitesse de balayage (Black et al., 2002; Shepherd et al., 2008). La normalisation des dispositifs DXA devient indispensable en raison des différences très importantes observées entre leurs résultats (Lantz et al., 1999).
L'équation prédictive de la MG (kg) de Lee et al. (2017) appliquée à notre échantillon donne une valeur moyenne surestimée significativement par rapport à la mesure exacte de la MG (kg) DXA.
Cependant, l'introduction d'un terme correctif peut être obtenu si l'on effectue une estimation de la MG sur un nombre limité de 5 sujets dont le BMI est comparable au BMI moyen de la population de Lee et al. (2017). Ce terme correctif de -4,2 kg, permet d'effectuer une translation de l'ensemble des valeurs de MG (kg). Dans ces conditions, il apparait que les écarts individuels de MG (kg) sont tout à fait superposables à ceux que nous avons obtenu su notre échantillon avec l'équation 1.
En ce qui concerne le pourcentage de graisse, il existe à nouveau une surestimation de 5,85% de MG% à partir de l'équation 4 de Lee. Après un réajustement de cette surestimation, on obtient des écarts individuels comparables entre notre estimation (équation 3) et celle de Lee corrigée.
Les mesures anthropométriques de Héo et al. (2013) sont en moyenne significativement supérieures à celle de notre échantillon. L'équation 6 de Héo et al. (2013) qui fait intervenir le BMI donne une prédiction surestimée de 4,65 kg de la MG(kg). En introduisant un terme correctif de 4,65 kg en choisissant 4 sujets dont le BMI est proche du BMI voisin de Héo et al. (2013), on obtient des écarts individuels équivalents à ceux obtenus avec l'équation 6.
Si l'on effectue une prédiction de la MG (kg) à partir d'une cohorte plus petite (n=271) comme celle de Larssen et al , on obtient à la fois une surestimation significative des valeurs moyennes et des écarts-types. Malgré l'introduction d'un facteur correctif, les écarts individuels présentent une dispersion très supérieure à celle obtenue par l'équation 1. Ainsi le modèle linéaire proposé par Larsson et al. (2006) n'est pas applicable à notre échantillon.
Il apparait ainsi que l'utilisation des équation prédictives élaborées à partir d'enquêtes épidémiologiques est applicable à notre échantillon sous réserve d'introduire un terme correctif inhérent aux réglages distincts antre les appareils de mesures DXA. Pour cela, il suffit de choisir judicieusement quelque sujets sont les caractéristiques anthropométriques sont proches de celles de la population de référence et de comparer les valeurs prédictives de MG (kg).
Dans le cas de la cohorte de Larsson et al. (2006), bien que la variabilité de la MG soit élevée (s =10,4 kg) son équation prédictive présente des écarts individuels trop élevés. Ceci est probablement lié au fait qu'il n'existe pas une variabilité suffisamment grande des mesures anthropométriques au voisinage de la moyenne de la masse grasse (kg) de l'échantillon de Larsson et al. (2006).
De nombreuse études ont effectuées des prédictions de la masse grasse à partir des mesures anthropométriques (Sun et al., 2010; Siobhan et al., 2013; Van der Ploeg et al., 2003). Gallagher et al. (2000) ont proposé une nouvelle approche potentielle pour développer des fourchettes de pourcentage de graisse corporelle. Les variables indépendantes de prédiction du pourcentage de graisse corporelle dans les modèles de régression multiple comprenaient 1/IMC, le sexe, l’âge et le groupe ethnique avec des valeurs R de 0,74 à 0,92 et des valeurs SEE de 2,8 à 5,4%. Cependant les effectifs proposés compris entre 94 et 99 restent trop faibles pour effectuer toute prédiction extrapolable.
En conclusion cette étude montre que l'utilisation des équations prédictives de la masse grasse et du pourcentage de graisse élaborées à partir de mesures anthropométriques au plan épidémiologique sont tout à fait applicables à différents échantillons pour lesquels les mêmes mesures anthropométriques ont été relevées. Cependant, compte tenu des différences de logiciel et de la vitesse de balayage des appareils de mesures DXA, il est impératif d'introduire un terme correctif. Pour cela, il faut relever les mesures de MG (kg) DXA en choisissant judicieusement un petit nombre de sujets ayant les mêmes caractéristiques anthropométriques que celles observées, en moyenne, de la population de référence dont les équations prédictives ont été élaborées sur de grands effectifs.
En définitive, il devient inutile de relevé la totalité des mesures de masse grasse DXA dans le cas d'une étude ponctuelle. Cette réduction du recueil des mesures DXA va engendrer une baisse significative des coûts pour un gain en précision des valeurs individuelles de masse grasse sensiblement équivalent.
Bibliographie
Black, E., Petersen, L., Kreutzer, M., Black, E., Petersen, L., Kreutzer, M., Toubro, S., Sørensen, T.I.A., Pedersen, O., Astrup, A., 2002, Fat mass measured by DXA varies with scan velocity. Obesity Research, 10, 69–77.
Gallagher, D., Heymsfield, S.B., Heo, M., , Jebb, S.A., Murgatroyd, P.R., Sakamoto, Y., 2000, Healthy percentage body fat ranges: an approach for developing guidelines based on body mass index. American Journal of Clinical Nutrition, 72, 694–701.
Héo, M., Kabat, G.C., Gallagher, D., Heymsfield, S.B., Rohan, T.E., 2013, Optimal scaling of weight and waist circumference to height for maximal association with DXA-measured total body fat mass by sex, age and race/ethnicity. International Journal of Obesity, 37, 1154–1160.
Kelly, T.L., Wilson, K.E., Heymsfield, S.B., 2009, Dual energyX-ray absorptiometry body composition reference values from NHANES. Plos one, 4, e7038.
Lantz, H., Samuelson, G., Bratteby, L.E., Mallmin, H., Sjöström, L., 1999, Differences in whole body measurements by DXAscanning using two Lunar DPX-L machines. International Journal of Obesity and Related Metabolic Disorders, 23, 764–770.
Larsson, I., Henning, B., Lindroos, A.K., Näslund, I., Sjöström, C.D., Sjöström, L., 2006, Optimized predictions of absolute and relative amounts of body fat from weight, height, other anthropometric predictors, and age. Am J Clin Nutr,8, 252–259.
Lee, D.H., Keum, N.N., Hu, F.B., Orav, E.J., Rimm, E.B., Sun, Q., Willett, W.C., Giovannucci, E.L., 2017, Development and validation of anthropometric prediction equations for lean body mass, fat mass and percent fat in adults using the National Health and Nutrition Examination Survey (NHANES) 1999–2006. British Journal of Nutrition, 118, 858–866.
Mills, T.C., 2008, Predicting body fat using weight—height indices. Journal of Applied Statistics, 35, 1131–1138.
Must, A., Spadano J., Coakley, E.H., Field, A.E., Colditz, G., Dietz, W.H., 1999, The disease burden associated with overweight and obesity. JAMA, 282, 1523–1529.
Newman, A.B., Sun Lee, J., Visser, M., et al., 2005, Weight change and the conservation of lean mass in old age: the Health,Aging and Body Composition Study. Am J Clin Nutr., 82,872–878.
Olshansky, S.J., Passaro, D.J., Hershow, R.C., et al., 2005, A potential decline in life expectancy in the United States in the 21st century. N Engl J Med., 352,1138–1145.
Shepherd, J.A., Morgan, S.L., Lu, Y., 2008, Comparing BMD results between two similar DXA systems using the generalized least significant change. Journal of Clinical Densitometry, 11, 237–242.
Siobhan, L., O'Neill, C., Sohun, R., Toomey, C., Jakeman, P., 2013, Generalised equations for the prdiction of percentage body fat by anthropometry in adult men and women aged 18-81 years. British Journal of Nutrition, 109, 678-685.
Sun, Q., Van Dam, R.M., Spiegelman, D., Heymsfield, S.B., Willett, W.C., Hu, F.B., 2010, Comparison of dual-energy X-ray absorptiometric and anthropometric measures of adiposity in relation to adiposity-related biologic factors. American Journal of Epidemiology, 172, 1442–1454.
Van der Ploeg, G.E., Gunn, S.M., Withers, R.T., Modra, A.C., 2003, Use of anthropometric variables to predict relative body fat determined by a four-compartment body composition model. European Journal of Clinical Nutrition , 57, 1009-1016.
WHO 2013, Factsheet: obesity and overweight: World Health Organization. http://www.who.int/mediacentre/factsheets/fs311/en/index.html.
Willett, W.C., Dietz, W.H., Colditz, G.A., 1999, Guidelines for healthy weight. N Engl J Med., 341, 427–434.
Wormser, D., Kaptoge, S., Di Angelantonio, E., Wood, A.M., Pennells, L.,Thompson, A., Sarwar, N., Kizer, J.R., Lawlor, D.A., Nordestgaard, B.G., et al., 2011, Separate and combined associations of body-mass index and abdominaladiposity with cardiovascular disease: collaborative analysis of 58 prospective studies. Lancet, 377,1085–1095.