Rebato, E., Rosique, J., Salces, I., San Martín, L., Fernández, J. R., Vinagre, A., 2002, Estudio comparativo entre el PB1 y la combinación del PB1 con el LMS en una muestra transversal de Bizkaia. Antropo, 3, 11-22. www.didac.ehu.es/antropo

---

Estudio comparativo entre el PB1 y la combinación del PB1 con el LMS en una muestra transversal de Bizkaia

Comparative study between PB1 and the combination of PB1 and LMS in a cross-sectional sample from Biscay

E. Rebato, J. Rosique, I. Salces, L. San Martín, J. R. Fernández, A. Vinagre

Departamento de Genética, Antropología Física y Fisiología Animal, Facultad de Ciencias, Universidad del País Vasco-EHU, Bilbao, España.

Correspondencia: Esther Rebato, Departamento de Genética, Antropología Física y Fisiología Animal, Facultad de Ciencias, Universidad del País Vasco-EHU, Apdo. 644 - 48080 Bilbao. España. E-mail: ggpreoce@lg.ehu.es

Palabras clave: Estatura, Crecimiento, LMS, PB1, Bizkaia.

Key words: Height, Growth, LMS, PB1, Biscay.

Resumen

Esta investigación tiene como objetivo analizar las diferencias introducidas por el ajuste de datos transversales de crecimiento mediante dos modelos diferentes: uno estructural, el PB1, y otro no estructural, el LMS. La combinación de ambos nos permitirá la construcción de curvas de crecimiento (estatura a cada edad) que servirán de referencia local para la provincia de Bizkaia. La muestra está constituida por 768 niños y 857 niñas de la provincia de Bizkaia con edades comprendidas entre los 7,5 y 18,5 años, a los que se les ha medido la estatura. Se han comparado los valores centilares suavizados independientemente mediante la aplicación del modelo 1 de Preece Baines (procedimiento A), con aquellos calculados aplicando el método LMS sobre la tendencia central de la muestra (procedimiento B), estimándose las diferencias porcentuales existentes entre los percentiles observados y los calculados mediante ambos procedimientos. La comparación con un estudio semi-longitudinal de la misma provincia, realizado en los años ochenta, apunta hacia una mayor estatura en la muestra vizcaína actual.

Abstract

The aim of this research is to analyze the differences introduced by the fitting of cross-sectional data of growth through of two different models: one structural, the PB1, and another one nonstructural, the LMS. The combination of both will allow the construction of growth curves (stature at each age) that will serve as local reference for the province of Biscay. 768 boys and 857 girls of the province of Biscay constitute the sample with ages between the 7.5 and 18.5 years, who has been sized. The smoothed centile values obtained by the application of model 1 of Preece Baines (procedure A) have been separately compared to those calculated applying the LMS method on the central tendency of the sample (procedure B). The percentage differences between the observed percentiles and the calculated ones by means of both procedures can be observed. The comparison with a semi-longitudinal study of the same area, carried out in the eighties, indicates a higher stature in the present sample of Biscay.

Introducción

El crecimiento puede ser definido como el proceso por el cual los individuos cambian en tamaño y forma a través de un cierto periodo de tiempo. Para analizar estos cambios se han venido utilizando curvas (“charts”) estandarizadas, basadas en la estatura, que permiten analizar el crecimiento individual. Sin embargo, los métodos de construcción de estándares, incluso referencias locales y nacionales, ha cambiado mucho en los últimos años. Originalmente, las curvas estaturales eran dibujadas y suavizadas manualmente por el investigador, pero actualmente las curvas que representan los cambios de la estatura frente a la edad (curvas de crecimiento) se obtienen utilizando metodologías estadísticas avanzadas basadas en el ajuste de modelos matemáticos. Una de las razones para la utilización de estos modelos es que constituyen una buena herramienta para predecir la talla adulta y la edad al PHV (Peak Height Velocity) o edad del estirón puberal, y para obtener una serie de parámetros biológicos que describen de forma más completa el proceso de crecimiento. De esta forma, un gran número de observaciones e información recogidas en el tiempo (en varios años, por ejemplo), y difíciles de interpretar en su conjunto, pueden ser resumidas en unos pocos y significativos parámetros.

Los distintos modelos matemáticos que se emplean para ajustar datos de crecimiento longitudinales y transversales pueden ser divididos en estructurales y no estructurales. Los modelos estructurales, como el Modelo I de Preece-Baines (PB1) (Preece y Baines, 1978) utilizado en este trabajo, dependen de un conjunto de parámetros, y se basan en el concepto de que el patrón de crecimiento tiene una forma funcional básica a la que se le puede atribuir una interpretación biológica directa. La desventaja de estos modelos es que están limitados a ciertos rangos de edad o a variables concretas, y no permiten describir sucesos particulares debido a la rígida configuración de la curva. Este tipo de funciones se usan normalmente para modelizar curvas de crecimiento individual más que para conjuntos de muestras o poblaciones. No obstante, pueden ser aplicadas a medias o a centiles seleccionados como la mediana o el percentil 90 (p90), de forma que pueden generarse curvas centilares suavizadas. Se ha demostrado que el PB1 permite generar estos centiles suavizados (Hauspie y Wachholder, 1986), describir mejor que ningún otro modelo matemático, el crecimiento puberal (Wember et al., 1992), y tener un número limitado de parámetros (cinco) que son relativamente fáciles de interpretar (Hauspie, 1989).

En cuanto a los modelos no estructurales, como el LMS (Cole, 1988, 1990), que también se ha utilizado en esta investigación, su ajuste permite igualmente una buena descripción del crecimiento, y constituye una buena aproximación para estimar centiles. Este tipo de modelos no imponen una estructura rígida predeterminada a las líneas centilares, y no sólo se aplican a variables que muestran un patrón de incremento monótono, como la talla o el peso, sino a otras variables menos “predecibles”, como el BMI (Body Mass Index o Índice de Masa Corporal) y los pliegues de grasa (Cole et al., 1995). Presentan, no obstante, el problema de no ser totalmente controlables en los extremos de los rangos de edad. La ventaja del método LMS, respecto a otros modelos no estructurales, es que permite estimar un pequeño número de parámetros interpretables biológicamente y puede ser usado para combinar referencias nacionales de crecimiento tanto como para construir una referencia internacional (Cole et al., 1998).

Aunque hasta la fecha han sido varios los autores que han utilizado el modelo PB1 para obtener curvas suavizadas de crecimiento mediante un ajuste independiente de las medias o de los percentiles observados (pe. Hauspie y Wachholder, 1986; Brown y Crisp, 1987; Zemel y Johnston, 1994; Rosique y Rebato, 1995), actualmente la mayoría de las investigaciones (Healy, 1992; Cole et al., 1998; Mei et al., 1998) utilizan métodos matemáticos que estiman todos los percentiles de forma simultánea a lo largo de la edad (Cole, 1988; Healy et al., 1988; Pan et al., 1990). Al aplicarse de esta forma el método, se establece entre las curvas centilares una relación que con el ajuste independiente no se conseguía, y el investigador tiene el control sobre la tendencia central, el grado de asimetría y la variabilidad.

Esta investigación tiene como objetivo analizar las diferencias introducidas por el ajuste de datos transversales de crecimiento mediante dos modelos diferentes: uno estructural, el PB1, y otro no estructural, el LMS. La combinación de ambos nos permitirá la construcción de curvas de crecimiento (estatura en cada edad) que servirán de referencia local para la provincia de Bizkaia. Para alcanzar este objetivo se han comparado los valores centilares suavizados independientemente mediante la aplicación del modelo 1 de Preece Baines (procedimiento A), con aquellos calculados aplicando el método LMS sobre la tendencia central de la muestra (procedimiento B), estimándose las diferencias porcentuales existentes entre los percentiles observados y los calculados mediante ambos procedimientos.

Material y Métodos

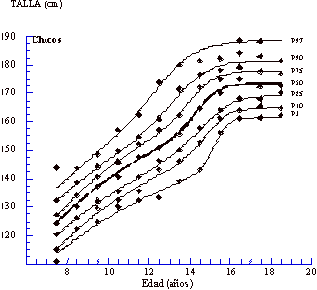
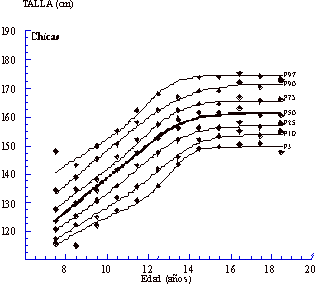
La muestra está constituida por 768 niños y 857 niñas de la provincia de Bizkaia, con edades comprendidas entre los 7,5 y 18,5 años de edad, a los que se les midió la estatura siguiendo los criterios del Programa Biológico Internacional (IBP, Weiner y Lourie, 1981). En este estudio se comparan las líneas centilares suavizadas (desde el p3 hasta el p97) obtenidas mediante la aplicación de dos procedimientos, con los percentiles obtenidos directamente de la muestra y con los obtenidos de una muestra local. El primer procedimiento de ajuste (A) consiste en deducir los percentiles suavizados de la estatura por edad aplicando el PB1 a los percentiles obtenidos directamente de la muestra. En el segundo procedimiento (B), se aplica el PB1 al conjunto de datos de la muestra obteniéndose una buena estimación de la talla media por edad. Con la estimación de esta curva se calculan las diferencias (residuos) que cada uno de los individuos posee con respecto a ésta. Aplicando el método LMS a estos residuos se obtienen simultáneamente todas las curvas centilares en función de la curva de tendencia central. Puesto que los modelos PB1 y LMS están ampliamente descritos en la literatura nos limitaremos a comentarlos brevemente:

Modelo I de Preece-Baines

Se trata de una función representada por 5 parámetros:

donde H₁ es la talla adulta, es una función del estirón del crecimiento puberal a lo largo del eje temporal, es el tamaño a la edad y S₀ y S₁ están relacionados con las velocidades prepuberal y puberal, respectivamente. El ajuste del PB1 se realizó por medio del procedimiento de regresión no linear (NLR) proporcionado por el paquete estadístico SPSS (9.0). La bondad del ajuste se comprobó mediante dos criterios complementarios: i) la obtención de la suma de cuadrados residuales (RSS) o su valor equivalente estandarizado (SEE), y ii) mediante la ejecución de un test RUNS sobre los residuos.

El método LMS

La siguiente ecuación expresa la estima de los centiles en función de la edad (T_j):

L(T_j)

donde L es el valor requerido para eliminar el sesgo de la muestra, M es el valor de la media, S es el coeficiente de variación y se corresponde con la desviación equivalente normal. Para medir la bondad del ajuste se ha empleado un test de c² tal y como recomiendan Cole et al. (1995). El ajuste del método LMS se realizó mediante un programa escrito en FORTRAN 77 (Cole y Green, 1992).

Comparación de ambos procedimientos

Procedimiento A: aplicando el PB1, se ajustan los centiles crudos observados uno a uno. De esta forma se estiman independientemente los centiles suavizados de cada categoría de edad.

Procedimiento B: aplicación del LMS sobre los residuos de la modelización de los valores centrales con otro modelo sobre el conjunto de los datos. El PB1 fue también un buen modelo opcional para conseguir esto ya que permite realizar una buena estimación de las tendencias centrales, es decir, la talla media a cada edad. 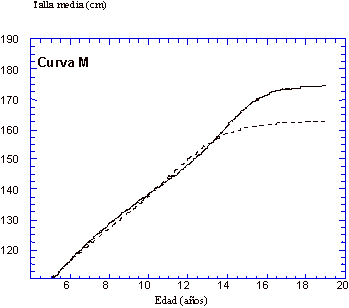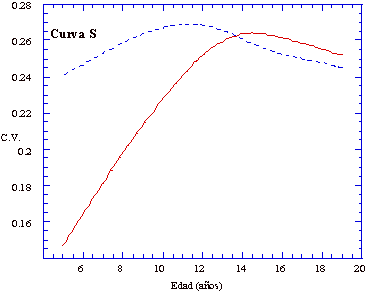Tras obtener esta curva central, se calcularon los residuos para todos los datos como la diferencia entre los valores observados y los esperados frente a la curva central, para cada edad. El resultado es un patrón de variación cambiante de la talla corporal con la edad. Como el método de Cole solamente admite valores positivos para calcular los centiles, los residuos obtenidos se transformaron añadiéndoles un factor de corrección: k, que sería cualquier valor adecuado mayor que cero:

Residuo transformado = residuo del PB1 + k

En un siguiente paso, se estimaron los centiles aplicando el método LMS sobre los residuos transformados. Finalmente, los valores centrales esperados del PB1 y los valores estimados para los residuos con el método LMS se sumaron para estimar, simultáneamente, el grupo de líneas centilares:

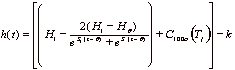
donde k es el mismo factor de corrección precedente.

Comparación entre centiles

Con el fin de analizar el grado de proximidad de los centiles del mismo rango, los valores centilares esperados por edad fueron comparados entre los procedimientos A y B, mediante un test Wilcoxon. Las diferencias entre los centiles suavizados obtenidos y los centiles crudos fueron también comparadas por un método basado en diferencias logarítmicas, mediante la fórmula:

100 * log (centil suavizado/centil crudo)

Esta ecuación se relaciona estrechamente con las diferencias porcentuales entre centiles (Cole 1989) y también ha sido aplicada al estudio de las discrepancias entre los procedimientos A y B mediante el cálculo de la formula logarítmica, situando a PB1 en el numerador. Los resultados obtenidos permiten asimismo comparar los centiles obtenidos de datos transversales con los de un estudio previo semi-longitudinal, realizado en una muestra de la misma provincia (Hernández et al., 1988).

Resultados y Discusión

Método A: aplicación del PB1 sobre las líneas centilares independientes

Los parámetros obtenidos de la aplicación independiente del modelo PB1 a cada línea centilar observada (3, 10, 25, 50, 75, 90 y 97), en ambos sexos, se muestran en la Tabla 1. La suma de cuadrados residuales (RSS) se sitúa, según la línea centilar considerada, entre el valor de 28,16 cm² (3^er centil) y 2,56 cm² (centil 25) para los chicos y entre 8,01 cm² (3^er centil) y 2,16 cm² (centil 25), para las chicas. Los valores de SEE se sitúan en el rango de variación de estudios precedentes (Lindgren y Hauspie, 1989; Rebato et al., 1993). En ambos sexos, el test de los RUNS para los residuos no fue significativo en ninguna línea centilar. Para todas las líneas centilares, la asíntota del modelo (h₁) se alcanzó a edades más precoces en las chicas que en los chicos. En éstos, el parámetro h₁, como se muestra en la Tabla 1, muestra un incremento a través de los distintos centiles: de 3,4 cm desde el centil 3 al 10, 4,5 cm del 10 al 25, 3,6 cm del 25 al 50, 4,6 cm del 50 al 75, 3,9 cm desde el 75 al 90 y 6,6 cm del 90 al 97. En las chicas los incrementos entre centiles son mayores que los de los chicos, excepto en el paso del centil 10 al 25 y del 90 al 97.

Centil ± SE
CHICOS	3		10		25		50		75		90		97
H1 (cm)	161,55	±1,33	164,9	±0,71	169,50	±0,49	173,13	±0,73	177,7	±0,6	181,67	±0,94	188,33	±1,13
HJ (cm)	152,38	±1,22	156,6	±0,68	159,98	±0,50	164,67	±0,74	169,0	±0,7	170,33	±1,51	175,05	±1,88
SJ(cm/año)	0,12	±0,02	0,15	±0,01	0,13	±0,01	0,15	±0,01	0,16	±0,0	0,13	±0,02	0,13	±0,02
S1 (cm/año)	3,03	±1,54	1,89	±0,39	1,32	±0,14	1,96	±0,49	1,78	±0,3	1,25	±0,28	1,16	±0,29
J (años)	15,25	±0,23	14,93	±0,16	14,84	±0,12	14,52	±0,17	14,19	±0,1	13,54	±0,26	12,76	±0,28
RSS (cm^2)	28,16		7,70		2,56		9,78		7,69		10,42		8,46
SEE (cm)	0,76		0,40		0,23		0,45		0,40		0,46		0,42
CHICAS	3		10		25		50		75		90		97
H1 (cm)	149,67	±0,58	154,1	±0,68	157,19	±0,43	161,02	±0,63	165,69	±0,6	171,78	±0,72	174,51	±0,72
HJ (cm)	141,52	±0,87	145,4	±1,36	147,12	±1,83	152,57	±2,19	156,41	±2,2	162,51	±2,66	166,12	±1,63
SJ(cm/año)	0,13	±0,02	0,13	±0,02	0,13	±0,03	0,16	±0,04	0,15	±0,0	0,15	±0,03	0,15	±0,03
S1 (cm/año)	1,94	±0,52	1,18	±0,27	0,98	±0,16	1,09	±0,29	1,18	±0,3	0,83	±0,24	1,55	±0,62
J (años)	13,21	±0,18	13,21	±0,31	12,36	±0,37	12,49	±0,47	12,31	±0,4	12,57	±0,62	12,16	±0,31
RSS (cm^2)	8,01		5,66		2,16		5,24		4,13		5,18		7,33
SEE (cm)	0,40		0,34		0,21		0,33		0,30		0,33		0,39

Tabla 1. Parámetros obtenidos del ajuste por PB1 del grupo de centiles observado en ambos sexos (SE = error estándar, RSS = suma de residuos cuadráticos, SEE = error estándar de la estima).

Table 1. Parameters obtained through the fitting by PB1 of the centile group observed in both sexes (SE = standard error, RSS = sum of squared residuals, SEE = estandar error of the estimation).

La Tabla 2 muestra los valores centilares suavizados finales obtenidos para las curvas de crecimiento de la muestra vizcaína. En general, los valores centilares encontrados para la edad fueron siempre mayores en chicos que en chicas, con algunas excepciones, como por ejemplo hasta la edad al PHV en los chicos (14,14 años, valor obtenido a partir de la primera derivada de la ecuación del modelo PB1). Cuando se observan los percentiles p25 y p50, los chicos son más altos que las chicas a casi todas las edades, excepto entre los 11,5 y los 13,5 años, debido al adelantamiento del estirón puberal en el sexo femenino respecto al masculino. Sin embargo, las chicas alcanzan estaturas más altas que los chicos a algunas edades en los centiles superiores (7,5 y 12,5 años para el p75, de 7,5 a 12,5 años para el p90 y desde los 7,5 a los 9,5 años para el p97), y en los centiles inferiores también (de 7,5 a 8,5 años y desde 13,5 a 14,5 años para el p3, y finalmente 7,5 años para el p10).

				Chicos							Chicas
Edad (años)	P3	P10	P25	P50	P75	P90	P97	P3	P10	P25	P50	P75	P90	P97
7,5	113,66	116,28	120,12	123,51	126,67	132,28	136,60	114,99	116,72	120,01	122,92	127,64	132,60	140,48
8,5	119,10	123,03	126,11	130,50	134,22	138,31	143,07	119,26	121,56	125,15	129,11	133,31	139,03	145,35
9,5	124,10	128,87	131,41	136,52	140,58	143,79	149,25	123,02	126,00	130,28	134,84	138,71	145,11	149,86
10,5	128,44	133,92	136,15	141,70	146,22	149,05	155,77	126,44	130,39	135,76	140,55	144,40	151,02	154,69
11,5	132,27	138,67	140,56	146,23	151,16	154,72	163,42	130,03	135,23	141,73	146,52	150,78	156,74	160,94
12,5	135,67	142,38	145,08	150,51	156,18	161,62	172,23	135,46	140,91	147,57	152,31	157,18	161,92	167,95
13,5	138,82	146,88	150,49	155,88	162,84	169,57	180,16	143,30	146,69	152,14	156,75	161,88	166,02	172,42
14,5	143,53	153,66	157,23	163,97	170,98	176,18	185,08	148,20	150,86	154,90	159,26	164,28	168,77	174,00
15,5	154,68	161,36	163,64	170,61	175,97	179,71	187,18	149,44	152,92	156,24	160,37	165,22	170,36	174,40
16,5	160,91	165,00	167,41	172,71	177,42	181,06	187,95	149,64	153,71	156,81	160,80	165,54	171,17	174,49
17,5	161,52	165,82	168,87	173,07	177,70	181,49	188,21	149,67	153,98	157,04	160,95	165,64	171,56	174,50
18,5	161,55	165,95	169,53	173,13	177,75	181,62	188,29	149,67	154,06	157,13	161,00	165,67	171,74	174,51

Tabla 2. Valores centilares suavizados de la estatura (cm) obtenidos por aplicación independiente del PB1 a cada línea centilar cruda (método A), en ambos sexos.

Table 2. Smoothed centile values of height (cm) obtained through the independent application of PB1 to each raw centile line (method A) n both sexes.

La Figura 1 muestra la representación gráfica de los centiles suavizados y crudos para la estatura por edades. La figura puede utilizarse como una gráfica de crecimiento cuando los datos observados se eliminan y sólo se representan las curvas centilares. El p50 muestra características relacionadas con la edad parecidas en chicos y en chicas. La distancia entre los centiles muestra una cierta variabilidad, dependiente de la edad, debido al ajuste independiente de las líneas. Estas distancias se incrementan, en chicas, desde los 11,5 a los 13,5 años, principalmente en los centiles extremos (p97 y p3), porque este rango de edad se produce también el mayor aumento de varianza estatural en chicas. En chicos se puede observar entre los 13,5 y los 15,5 años un aumento paralelo de la varianza estatural, debido a que, a esas edades, las curvas centilares masculinas también han incrementado las distancias entre ellas.

Figura 1. Curvas de crecimiento obtenidas por ajuste independiente con PB1 de las líneas centilares crudas (método A) en ambos sexos. También se muestran los valores centilares crudos (¨).

Figure 1. Growth charts obtained by the independent fiting with PB1 of the raw centile lines (method A) in both sexes. The raw centile values are also showed.

Método B: aplicación del LMS sobre los residuos de los valores centrales

El PB1 se utilizó para modelizar los valores centrales en la muestra total antes de aplicar el LMS. El ajuste del PB1 se consideró bueno debido a los valores de SEE (0,27 en chicos y 0,22 en chicas), y la distribución aleatoria de los residuos. De hecho, para ambos sexos, el test de los RUNS confirmó una desviación no significativa de los residuos. Los parámetros finales del PB1 para los valores centrales fueron los siguientes:

Chicos: h₁ = 173,94 ± 0,78, h_J = 164,73 ± 0,78, s₀ = 0,14 ± 0,01, s₁ = 1,42 ± 0,24, J = 14,55 ± 0,17.

Chicas: h₁ = 162,57 ± 0,66, h_J = 151,29 ± 3,41, s₀ = 0,12 ± 0,05, s₁ = 0,85 ± 0,20, J = 12,26 ± 1,68.

La primera derivada de la ecuación del modelo ha permitido extraer los principales parámetros biológicos que caracterizan el crecimiento estatural en la muestra masculina (edad al inicio del estirón: 11,34 años, estatura al inicio del estirón: 145,47 cm, velocidad al inicio del estirón: 4,61 cm/año, edad al PHV: 14,14 años, estatura al PHV: 161,73 cm, velocidad al PHV: 7,57 cm/año), y de la muestra femenina (edad al inicio del estirón: 8,03 años, estatura al inicio del estirón: 127,12 cm, velocidad al inicio del estirón: 5,27 cm/año, edad al PHV: 11,08 años, estatura al PHV: 144,35 cm, velocidad al PHV: 6,08 cm/año).

La Tabla 3 muestra los valores individuales de los parámetros L, M y S, obtenidos de los residuos y la M transformada en el ajuste por edades, teniendo en cuenta la cantidad independiente de información presente en la muestra total, es decir, 544 y 567 valores estaturales para chicos y chicas, respectivamente. La curva M tenía 25 edf (equivalent degrees of freedom) para los chicos y 22 edf para las chicas, con curvas S de 3 edf para chicos y 3 edf para chicas, ajustados sobre la escala de edad no transformada. Como el coeficiente de variación obtenido (CV) para la estatura es pequeño, el efecto sobre la desviación de los centiles fue mínimo, por lo que el valor inicial de L se fijó en 1. Tras el ajuste, la transformación de Box-Cox (L) proporcionó un valor de 0,706 para chicos y 0,847 para chicas (Tabla 3), estableciendo que, de hecho, no había grandes evidencias de sesgo, porque como se esperaba L se mantenía muy próxima a 1. La bondad del ajuste se probó por medio de un test de c² para controlar que la dispersión de los valores no mostrase diferencias significativas entre el número de puntos observado y esperado (c² con 7 g.l. fue de 6,642 para chicos y 6,509 para chicas).

	Chicos (L=0,706)				Chicas (L=0,847)
Edad años		M	S	M transf. (cm)	M	S	M transf. (cm)
7,5		25,032	0,231	124,24	22,122	0,286	124,35
8,5		25,046	0,247	130,54	22,098	0,291	129,65
9,5		25,063	0,264	136,59	22,074	0,296	135,05
10,5		25,080	0,278	141,20	22,054	0,299	140,60
11,5		25,101	0,294	145,99	22,036	0,301	146,99
12,5		25,115	0,306	151,09	22,022	0,301	152,55
13,5		25,115	0,313	156,98	22,011	0,298	156,75
14,5		25,103	0,314	164,03	22,002	0,295	159,77
15,5		25,076	0,310	170,20	21,994	0,291	161,21
16,5		25,041	0,304	172,78	21,986	0,288	161,96
17,5		24,992	0,297	173,64	21,979	0,286	162,29
18,5		24,936	0,290	173,86	21,972	0,284	162,44

Tabla 3. Valores LMS derivados de la muestra vizcaína para la L de Box-Cox y la media M para los residuos, el coeficiente de variación S y la M transformada, por sexos y edades.

Table 3. LMS values derived from the Biscay sample for the Box-Cox’s L and the mean M of the residuals, the coefficient of variation S and the transformed M value, for each sex and age.

La Figura 2 muestra las representaciones gráficas de las curvas S y M ajustadas para la muestra estudiada frente a la edad. La curva S de los chicos mostró que el CV de la estatura aumentaba con la edad desde los 14,0 a los 14,5 años de edad, donde se encuentra la edad al PHV previamente obtenida (14,14 años) a partir de la primera derivada del PB1. Con un patrón similar de crecimiento al de la curva S de chicos, la de las chicas aumentaba bastante uniformemente hasta un pico más ancho, correspondiente a su pubertad, en el rango entre 11 y 12 años de edad (donde se encuentra la edad al PHV de las chicas, 11,08 años), y después descendía. La Tabla 4 muestra los valores centilares suavizados obtenidos al aplicar el método B. Como se mostró con el método A, los chicos siempre eran más altos que las chicas en todos valores centilares equivalentes, con algunas excepciones. En ambos métodos (A y B), los valores centilares finales del p25 mostraban tallas más altas en chicas en el mismo rango de edad (de 11,5 a 13,5 años). Los otros centiles tenían un patrón similar de solapamiento (longitud y situación de los rangos de edad solapados) en el método B (Tabla 4) con respecto al método A (Tabla 2), aunque con ligeras variaciones. El método B mostró también el principal solapamiento antes de que los chicos llegasen a la edad al PHV (11,5 años y 12,5 años desde el p3 al p75, y a los 13,5 años del p3 al p25), y al inicio del rango de edad (7,5 años para p50, p90 y p97).

Figura 2. Comparación de las curvas S y M transformadas por edades y en ambos sexos. Los valores para chicos se muestran como líneas continuas, con líneas discontinuas para las chicas. CV = Coeficiente de variación.

Figure 2. Comparison of S and M curves transformed for each age and sex. Values of boys are showed as continuous lines, and those for girls with dotted lines. CV = coefficient of variation.

				Chicos							Chicas
Edad (años)	P3	P10	P25	P50	P75	P90	P97	P3	P10	P25	P50	P75	P90	P97
7,5	114,14	117,20	120,47	124,24	128,27	132,00	135,81	113,14	116,62	120,27	124,35	128,79	132,78	136,79
8,5	119,81	123,05	126,52	130,54	134,85	138,86	142,96	118,25	121,77	125,48	129,65	134,15	138,21	142,29
9,5	125,20	128,62	132,31	136,59	141,22	145,53	149,94	123,46	127,03	130,79	135,05	139,59	143,71	147,86
10,5	129,25	132,83	136,71	141,20	146,12	150,67	155,36	128,87	132,47	136,28	140,60	145,17	149,33	153,53
11,5	133,46	137,20	141,27	145,99	151,20	156,03	161,00	135,18	138,80	142,62	146,99	151,56	155,75	159,97
12,5	138,08	141,95	146,18	151,09	156,55	161,61	166,82	140,76	144,37	148,18	152,55	157,11	161,29	165,50
13,5	143,71	147,65	151,96	156,98	162,57	167,75	173,09	145,03	148,62	152,40	156,75	161,25	165,40	169,58
14,5	150,71	154,66	158,98	164,03	169,62	174,81	180,17	148,19	151,73	155,47	159,77	164,21	168,30	172,42
15,5	157,04	160,94	165,20	170,20	175,67	180,78	186,04	149,74	153,25	156,95	161,21	165,59	169,63	173,70
16,5	159,84	163,67	167,86	172,78	178,10	183,10	188,24	150,59	154,07	157,73	161,96	166,28	170,28	174,31
17,5	160,93	164,69	168,78	173,64	178,78	183,65	188,66	151,00	154,45	158,09	162,29	166,57	170,53	174,53
18,5	165,06	165,06	169,06	173,86	178,82	183,56	188,43	151,23	154,66	158,27	162,44	166,68	170,61	174,58

Tabla 4. Valores centilares suavizados obtenidos al aplicar el método LMS a los residuos de las tendencias centrales de los datos (método B).

Table 4. Smoothed centile values obtained through the application of the LMS method to the residuals of the central tendencies of the data (method B).

La Tabla 5 muestra el porcentaje de discordancia entre los dos grupos de curvas en las representaciones gráficas de las referencias del crecimiento por sexos. El p3 y el p97 mostraron el mayor desacuerdo entre métodos en ambos sexos. El sesgo sistemático entre líneas centilares fue, en general, ligeramente mayor en chicas que en chicos. El test de Wilcoxon mostró evidencias significativas entre los métodos A y B (p < 0,01), únicamente en el p3 y el p25 en chicos y en todos los centiles, excepto el p3, en chicas. En chicos, en general, los centiles 3 y 25 eran más altos con el LMS que con el PB1. Mientras en chicas, por encima del p75 los valores del LMS eran en general más altos que los esperados por el PB1; en general, después de los centiles 90 y 97 aparecen valores más altos en el PB1.

			P3	P10	P25	P50	P75	P90	P97	Global
CHICOS	PB1	m	0,013	-0,292	0,018	0,028	0,030	0,085	0,091	-0,004
	(método A)^1	s	0,568	0,320	0,153	0,263	0,216	0,301	0,854	0,445
	LMS	m	-0,570	-0,190	-0,200	-0,040	-0,070	-0,110	0,520	-0,094
	(método B)^1	s	0,916	0,382	0,216	0,300	0,304	0,446	0,992	0,640
	Entre	m	-0,585	0,098	-0,215	-0,066	-0,102	-0,196	0,434	-0,090
	métodos	s	0,682	0,266	0,182	0,144	0,225	0,347	0,652	0,491
CHICAS	PB1	m	-0,092	0,088	0,085	0,105	0,057	-0,047	0,017	0,030
	(método A)^1	s	0,559	0,246	0,171	0,257	0,353	0,390	0,844	0,445
	LMS	m	-0,510	-0,290	-0,110	-0,090	-0,110	0,190	0,450	-0,067
	(método B)^1	s	0,744	0,450	0,175	0,284	0,303	0,396	1,015	0,607
	Entre	m	-0,415	-0,381	-0,190	-0,200	-0,165	0,233	0,434	-0,098
	métodos	s	0,714	0,393	0,078	0,160	0,160	0,140	0,378	0,451

Tabla 5. Descriptivos (m = media, s = desviación estándar) de las diferencias porcentuales entre los centiles observados empíricamente y los esperados en la modelización, tras aplicar ambos métodos (PB1 y LMS) en chicos y chicas. También se muestran las diferencias globales entre los centiles y la discordancia entre métodos.

¹ = con respecto a los centiles crudos

Table 5. Descriptive statistics (m = mean valued, s = standard deviation) of the percentage differences between the observed centiles and those expected from the modellisation, after the application of both methods (PB1 and LMS) in boys and girls. The whole differences between the centiles and the difference between both methods are also showed.

¹ = considering raw centiles

La proximidad de los valores centilares obtenidos con los métodos A y B en los datos centilares crudos también se estudió calculando el porcentaje de desacuerdo entre centiles (Tabla 5). Cuando se comparan todos los porcentajes entre centiles, el PB1 podría ajustar ligeramente mejor los datos crudos que el LMS en ambos sexos. Sin embargo, el p10 en chicos tenía el mayor grado de discordancia (-0,292%), incluso aplicando el ajuste LMS (-0,190%). El grado de discordancia con respecto a los datos crudos fue bastante homogéneo entre centiles cuando se ajustaban con PB1, mientras que el porcentaje de discordancia cuando se utilizaban los métodos A y B estaba próximo al 0,1% en valores absolutos con los centiles extremos (p3 y p97), los menos concordantes de todos.

El porcentaje de discordancia entre los centiles suavizados de los datos transversales de la muestra vizcaína y los presentados por Hernández et al. (1988), de una muestra del Gran Bilbao, se obtuvo aplicando también diferencias logarítmicas. Las diferencias porcentuales globales entre centiles eran ligeramente menores cuando se utilizaban los centiles suavizados del PB1 (0,339% para chicos y 0,454% para chicas) que cuando se utilizaban los centiles suavizados del LMS (0,594% para chicos y 0,394 para chicas). Sin embargo, casi todas las diferencias por edades eran mayores que cero en ambos métodos, principalmente con el LMS, excepto en el percentil más bajo (p3) a algunas edades. Por lo tanto, a partir de esta comparación puede sugerirse un cambio hacia arriba en las líneas centilares de las curvas de crecimiento en la población vizcaína actual.

Agradecimientos. Esta investigación ha sido parcialmente financiada por una Ayuda a la Investigación de la Sociedad de Estudios Vascos – Eusko Ikaskuntza.

Bibliografía

Brown, S., y Crisp, J., 1987, Observation of the changes in standing height at the time of puberty. Annals of Human Biology, 14, 449-452.

Cole, T.J., 1988, Fitting smoothed centile curves to reference data. Journal of the Royal Statistical Society, 151, 385-418.

Cole, T.J., 1989, Using the LMS method to measure skewness in the NCHS and Dutch National height standards. Annals of Human Biology, 5, 407-419.

Cole, T.J., 1990, The LMS method for constructing normalized growth standards. European Jorunal of Clinical Nutrition, 44, 45-60.

Cole, T.J., Freeman, J.V., y Preece, M.A., 1995, Body Mass Index reference curves for the UK. Archives of Disease in Childhood, 73, 25-29.

Cole, T.J., Freeman, J.V., y Preece, M.A., 1998, British 1990 growth reference centiles for weight, height, body mass index and head circumference fitted by maximum penalized likelihood. Statistics in Medicine, 17, 407-429.

Cole, T.J., y Green, P.J., 1992, Smoothing reference centile curves: the LMS method and penalized likelihood. Statistics in Medicine, 13, 2359-2367.

Hauspie, R.C, 1989, Modèles structurels dans l’analyse de la courbe de croissance. Anthropologie et Prèhistoire, 100, 123-128.

Hauspie, R.C., y Wachholder, A., 1986, Clinical standards for growth velocity of Belgian boys and girls, aged 2 to 18 years. International Journal of Anthropology, 1, 339-348.

Healy, M.J.R., 1992, Normalising transformations for growth standards. Annals of Human Biology, 19, 521-526.

Healy, M.J.R., Rasbash, J., y Yang, M., 1988, Distribution-free estimation of age-related centiles. Annals of Human Biology, 15, 17-22.

Hernández, M., Castellet, J., Narvaíza, J.L., Rincón, J.M., Ruiz, I., Sánchez, E., Sobradillo, B., y Zurimendi, A., 1988, Curvas y Tablas de Crecimiento. En Instituto de Investigación sobre Crecimiento y Desarrollo. Fundación F. Orbegozo (Madrid: Garsi).

Lindgren, G.W., y Hauspie, R.C., 1989, Heights and weights of Swedish school children born in 1955 and 1967. Annals of Human Biology, 16, 397-406.

Mei, Z., Yip, R., Grummer-Strawn, L.M.,, Trowbridge, F.L., 1998, Development of a research child growth reference and its comparison with the current international growth reference. Archives of Pediatric and Adolescent Medicine, 152, 471-479.

Pan, H., y Goldstein, H., 1997, Multi-level models for longitudinal growth norms. Statistics in Medicine, 16, 2665-2678.

Pan, H.Q., Goldstein, H., y Yang, Q., 1990, Non-parametric estimation of age-related centiles over wide age ranges. Annals of Human Biology, 17, 475-481.

Preece, M.A., y Baines, M.J., 1978, A new family of mathematical Models describing the human growth curve. Annals of Human Biology, 5, 1-24.

Rebato, E., González, A., y Rosique, J., 1993, Application du modèle I de Preece-Baines (PB1) à l’étude de la croissance staturale chez deux populations biscaïennes. Bulletins et Mémoires de la Societé d’Anthropologie de Paris, 5, 93-102.

Rosique, J., y Rebato, E., 1995, Comparative study of statural growth in Spanish populations. American Journal of Human Biology, 7, 553-564.

Weiner, J.S., y Lourie, J.A., 1981, Practical Human Biology. (Londres: Academic Press).

Wember, T., Goddemeier, T., y Manz, F., 1992, Height growth of adolescent German boys and girls. Annals of Human Biology, 4, 361-369.

Zemel, B.S., y Johnston, F.E., 1994, Application of the Preece-Baines growth Model to cross-sectional data: Problems of validity and interpretation. American Journal of Human Biology, 6, 563-670.