Colloques du Groupement des Anthropologistes de Langue Française (GALF)

Martins, R., Schmitt, A., Oliveira, P.E., 2012, Révision de la méthode proposée par Schmitt (2005) pour estimer l’âge au décès des adultes à partir de la surface sacro-pelvienne iliaque. Antropo, 27, 57-61. www.didac.ehu.es/antropo

 

Révision de la méthode proposée par Schmitt (2005) pour estimer l’âge au décès des adultes à partir de la surface sacro-pelvienne iliaque

 

R. Martins¹, A. Schmitt², P.E. Oliveira³

 

¹Centro de Investigação Interdisciplinar Egas Moniz (ciiEM) Caparica – Portugal

²Anthropologie bioculturelle (UMR 6578) Marseille - France

³CMUC, Departamento de Matemática, Universidade de Coimbra, Coimbra - Portugal

 

Auteur Correspondant: Aurore Schmitt, CNRS, UMR 6578- Anthropologie bioculturelle
Faculté de Médecine - Secteur Nord, Université de la Méditerranée, CS80011, Bd Pierre Dramard 13 344 Marseille Cedex 15

 

Mots clés: Estimation de l’âge au décès, Adulte, «Kernel density», Surface auriculaire de l’ilium.

 

Key words: Age-at-death assessment, Adult, Kernel density, Auricular surface of the ilium.

 

Résumé

La surface auriculaire de l’ilium a fait l’objet de nombreuses méthodes pour estimer l’âge au décès des adultes. En 2005, Schmitt proposait un système de cotation simple (4 critères morphologiques avec 2 à 4 modalités), l’utilisation de probabilités, l’aggrégation de plusieurs séries européennes d’âge connu et un intervalle chronologique plutôt qu’un âge précis, pour une estimation sur les échantillons archéologiques. Cette méthode permet d’identifier les individus décédés après 60 ans, ce qui n’est pas le cas des méthodes classiques, et privilégie la fiabilité à la précision. Toutefois,  la limite majeure est l’impossibilité d’estimer l’âge de certains sujets. Les données ont été traitées par une autre approche statistique basée sur l'estimateur du noyau de la densité (« kernel density procedure »), tenant compte des observations au voisinage de chaque point. Ce nouveau système permet une approximation de l'âge de tous les individus et des intervalles chronologiques moins larges que ceux proposés dans la méthode initiale.

 

Abstract

  The auricular surface of the ilium has been largely used as the basis for age-at-death assessment methods. In 2005, Schmitt proposed a simple scoring system (4 features with 2 to 4 phases), the use of a probability estimation procedure, the aggregation of several European series with known age and sex, and the estimation of a credible chronological interval rather than a numerical estimation of age. This method enables identification of individuals deceased after 60 years, but with the drawback of not being able to produce an approximation for many of them. The same data was later processed using another statistical approach, based on smoothing methods.  The probability distribution and the conditional distribution are estimated from training data using discretized kernel density procedures. This approach produces an age for all the individuals and the credible intervals are narrower than the initial method.

 

Introduction

La surface sacro-pelvienne iliaque a fait l’objet de nombreuses méthodes pour estimer l’âge au décès des adultes (Lovejoy et al., 1985; Buckberry et Chamberlain, 2002, Ygarashi et al., 2005). Chacune de ces méthodes a été élaborée sur une seule série ostéologique d’âge connu et ne tiennent pas compte de l’influence de la population de référence. La méthode proposée par Schmitt (2005) se base sur l’étude de la variabilité des modifications de la surface sacro-pelvienne iliaque sur plusieurs série d’Europe, d’Asie, d’Amérique et d’Afrique. De plus, sa fiabilité a été testée sur des échantillons complètement indépendants du référentiel. Le système de cotation est simple, l’estimation de l’âge au décès est menée par un calcul de probabilités (Lucy et al., 1996), la population de référence consiste en l’agrégation de plusieurs séries européennes d’âge connu. Cette méthode permet d’identifier les individus décédés après 60 ans (ce qui n’est pas le cas des méthodes classiques) et privilégie la fiabilité à la précision. Toutefois,  l’impossibilité d’estimer l’âge de certains sujets confère à la méthode un inconvénient majeur. C’est la raison pour laquelle une nouvelle approche statistique a été mise en œuvre.

 

Matériel et méthode

Le système de cotation est publié dans l’article princeps (Schmitt, 2005). Trois séries utilisées dans la méthode initiale ont été utilisées dans la présente étude. Elles sont issues de la collection identifiée de l’Université de Coimbra au Portugal (Rocha, 1995), de la collection de Spitalfields en Angleterre (Molleson et Cox, 1993) et de la collection Hammann-Todd à Cleveland aux Etats-Unis (Mensforth et Latimer, 1989). La composition du corpus est présentée dans le tableau 1. Les deux sexes sont représentés et la distribution par âge est homogène.    

 

Tableau 1. Effectif des individus par collection ostéologique.

 

L’approche statistique étant développée par ailleurs (Martins et al., 2011), nous la présentons brièvement. Le traitement des données commence par une décomposition Bayesiènne de la distribution. L’estimation se base sur la méthode du noyau, avec des adaptions appropriées pour les variables discrètes, inspirée par Lucy et al. (1996). Répresentons par  l’age de l’individu et par  les  caractères morphologiques. D’après le Théorème de Bayes, la distribution par âge connaissant les caractères observés  est:

                                                                                                    (1)

oú est la vraisemblance des caractères quand l’âge est connu , et  est la distribution de . La distribution marginale des caractères , peut s’estimer en additionnant par rapport à  le numérateur de (1).

La caractérisation de  est délicate car cette fonction dépend des relations entre les variables. Une première approche, très simplifiée, suppose que lorsque que l’âge est connu, les caractères sont statistiquement indépendants. On appelle ce modèle indépendance  conditionnelle. La vraisemblance peut donc s’écrire ainsi:

                                                                                                      (2)

oú  est la vraisemblance individuelle de la distribution du caractère  admettant l’age connue . Um modèle plus realiste, appelé dépendance conditionnelle, doit inclure la dépendance entre les caractères. Pour mesurer cette dépendance nous utilisons une méthode proposée par Chow and Liu (1968): il s’agit de construire un arbre de dépendance décrivant le parcours reliant les caractères. On désigne, aléatoirement, un caractère pour point de départen dehors duquel, tout caractère  a un progéniteur désigné par . Ainsi, la fonction de vraisemblance peut se décomposer de la façon suivante:

                                                                                               (3)

oú  est la valeur observée pour le progeniteur de . Pour le point de départ, ,.

En ce qui concerne la construction d’estimateurs pour les distributions considerées, nous utilisons la méthode du noyau (Silverman, 1986; Wand and Jones, 1995). Pour la densité de l’age , on calcule:

                                                                               (4)

oú les , , et  est une fonction non-négative telle que . Pour la fonction  nous prennons le noyau Gaussian, bien connu pour ses propriétés quasi-optimales et la simplification des aspects calculatoires. Le choix de la fenêtre a plus d’impact sur les estimations. Pour cet aspect, nous avons suivi la procédure de Silverman (1986):

                  (5)

Ce choix est approprié du point de vue calculatoire et donne des résultats satisfaisants pour une grande variété de distributions.

Le traitment de la distribution des caractères est un peu plus délicate car elle est discrète, donc les versions multi-dimensionelles de l’estimateur (4) doivent prendre cet aspect en considération. En admettant l’âge  continu et les caractères discrets, nous estimons la distribution conjointe avec:

                                                                            (6)

oú  est un noyau (Gaussian),  une fenêtre indépendente de ,  si et  pour toutes les autre valeurs de , et  fait le comptage du nombre d’observations avec les caractères égaux à . Cette expression correspond à l’estimation de plusieurs distributions condionnelles (figure 1).

 

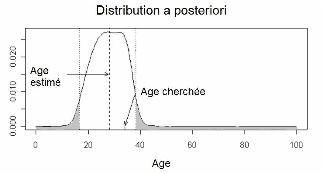
Figure 1. Distribution a posteriori de l’âge estimé d’un individu dont l’âge réel est 28 ans.

                                                                      

Ce traitement a été appliqué sur chacune des trois échantillons séparément puis sur le corpus total. L’analyse a été menée avec le Logiciel R.

 

Résultats

Les résultats sont présentés dans le tableau 2. Quel que soit le set de données considéré, l’application de l’hypothèse d’une dépendance conditionnelle des caractères observés permet d’obtenir des écarts absolus moyen (EAM), des biais et des intervalles d’âge estimé (IE) moins élevés et donc plus fiables que l’utilisation de l’hypothèse d’indépendance conditionnelle. Le pourcentage d’intervalle fiable (incluant l’âge réel des individus) est plus élevé pour cette dernière, mais ce résultat est lié au fait que les intervalles sont beaucoup plus grands. Les biais oscillent entre 0.3 et 0.45.

Dans les trois séries considérées séparément, les intervalles d’âge estimé sont plus larges pour les femmes et pour la série de Spitafields, mais pas nécessairement plus fiables (PI). Lorsque les trois échantillons sont réunis dans l’analyse, IE et PI sont sensiblement les mêmes quelle que soit la modalité de la variable sexe (homme/femme, indéterminé), mais moins fiables que lorsque les séries sont analysées séparément.

 

Tableau 2. Résultats pour les 3 échantillons séparés et le corpus complet selon le sexe. EAM: écart absolu moyen;

IE: taille de l’intervalle estimé; PI: pourcentage des intervalles (à 95%) qui incluent l’âge réel.

 

Discussion

L’analyse statistique montre que les caractères observés ne sont pas indépendants entre eux et qu’en tenant compte de ce paramètre, la fiabilité est accrue.

Les biais sont globalement élevés ce qui montre que l’âge des individus jeunes est surestimé et celui des plus âgés sous-estimé.

L’approche statistique proposée permet d’estimer l’âge au décès (sous forme d’intervalle chronologique fiable) de tous les individus ce qui n’était pas le cas de la méthode initiale dont la technique statistique paramétrique était conditionnée par des classes d’âge prédéfinies.

Globalement, l’estimation de l’âge si le sexe de l’individu est connu est plus fiable.

Le script R permettant d’appliquer ce traitement statistique est accessible sur demande (aurore.schmitt@univmed.fr). Il permet d’estimer l’âge en fonction du sexe (une modalité indéterminée est prévue) et de la population d’origine (si elle est connue).  Pour l’application sur du matériel archéologique, la compilation des 3 séries compose le corpus de référence.

 

Références bibliographiques

Buckberry J.L., Chamberlain A., 2002, Age Estimation from the auricular surface of the ilium: a revised method.  American Journal of Physical Anthropology, 119, 231-329.

Chow CK., Liu CN., 1968, Approximating Discrete Probability Distributions with Dependence Trees. IEEE Transactions on Information Theory, 14, 462-467.

Igarashi Y., Kagumi U., Tetsuaki W., Kanazawa E., 2005, New method for estimation of adult skeletal age at death from the morphology of the auricular surface of the ilium. American Journal of Physical Anthropology, 128, 324-339.

Lovejoy C.O., Meindl R.S., Prysbeck T.R., Mensforth R.P., 1985, Chronological metamorphosis of the auricular surface of the ilium: a new method for the determination of adult skeletal age at death. American Journal of Physical Anthropology, 68, 15-28.

Lucy D., Aykroyd R.G., Pollard A.M., Solheim T., 1996, A Bayesian approach to adult human age estimation from dental observations by Johanson's age changes. Journal of Forensic Sciences, 41, 189-194.

Martins R., Oliveira P. E., Schmitt A., Estimation of age at death from the pubic symphysis and the auricular surface of the ilium using a smoothing procedure. Forensic Science International, in press.

Mensforth R.P., Latimer B.M., 1989, Hamann-Todd Collection aging studies: osteoporosis fracture syndrome. American Journal of Physical Anthropology, 80, 461-479.

Molleson T., Cox M., 1993, The Spitafields project, volume 2, the Anthropology. Council for British Archaeology Research Report, 86, 167-179.

Rocha M.A., 1985, Les collections ostéologiques humaines identifiées du Musée Anthropologique de l’Université de Coimbra. Antropologia Portuguesa, 13, 7-38.

Schmitt A., 2005, Une nouvelle méthode pour estimer l’âge au décès des adultes à partir de la surface sacro-pelvienne iliaque. Bulletins et Mémoires de la Société d’Anthropologie de Paris, 17, 89-101.

Silverman B.W., 1986, Density estimation for statistics and data Analysis. (Londres:Chapman and Hall).

Wand M.P., Jones M.C., 1995, Kernel Smoothing (Londres: Chapman and Hall).